Составим математическую модель задачи. Обозначим через xij искомый объем перевозки от поставщика I к потребителю j и будем рассматривать переменные xij, задающие план перевозок, как компоненты матрицы перевозок X размеров :

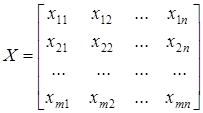. (13)

Затраты, связанные с некоторой перевозкой xij, составляют величину cijxij, а общая стоимость перевозок z от всех поставщиков ко всем потребителям определится равенством:

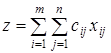. (14)

В соответствии с постановкой задачи план перевозок должен быть составлен так, чтобы вывоз от каждого поставщика равнялся его объему производства:

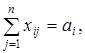
(15)

а общие поставки любому потребителю удовлетворяли его спрос:

(16)

Из физического смысла переменных следуют условия их неотрицательности

(17)

В итоге получаем формулировку транспортной задачи: найти значения переменных xij, удовлетворяющие условиям (15) – (17) и минимизирующие целевую функцию (14). Это каноническая задача линейного программирования. В ней число переменных равно mn, число ограничений-равенств – m+n.

Левые части уравнений (15) образованы строчными , а уравнений (16) – столбцовыми элементами матрицы перевозок (13). В соответствии с условиями (15) и (16) сумма элементов i-й строки матрицы Х должна быть равна ai, а сумма элементов j-го столбца – bj. В дальнейшем будем называть уравнения (15) строчными, (16) – столбцовыми.

Для проверки условий совместности системы (15), (16) проведем суммирование уравнений (15) по индексу I, а (16) – по j. Получаем равенства

; ,

левые части которых отличаются только порядком суммирования. Следовательно, они равны между собой. Тогда будут равны и правые части

(18)

Условие (18) является условием совместимости системы ограничений (15) – (16). Оно выражает требования баланса между суммарными запасами и суммарными потребностями.

Транспортную задачу, для которой выполняется условие баланса (18), называют закрытой задачей. Если же условие нарушено, то задача называется открытой. Здесь возможны два случая:

а) суммарные запасы превышают суммарный спрос;

б) суммарный спрос больше суммарных запасов.

В первом случае после удовлетворения спроса всех потребителей у некоторых поставщиков останется невывезенный продукт, во втором случае поставки для некоторых потребителей будут меньше их потребности.

При построении модели в первом случае для совместности условий строчные ограничения должны быть записаны как ограничения-неравенства, допускающие неполный вывоз имеющегося продукта. Модель примет вид

; (19)

;

;

Аналогично во втором случае неравенствами должны быть выражены столбцовые ограничения, допускающие неполное удовлетворение спроса.

Открытая модель легко сводится к эквивалентной ей закрытой модели. Так, в первом случае введем фиктивный потребитель с величиной спроса

Другое по теме:

Редуктор с конической передачей с карданным валом
Механизм для перестановки крыльев необходим для изменения угла стреловидности на современных многорежимных самолетах, способных летать на различных скоростях. Для каждой скорости полета существует оптимальная конфигурация крыла, которая зависит от его стреловидности. Для уменьшения сопро ...

Технология и организация автомобильных перевозок
Транспортный процесс – совокупность организационно и технологически взаимосвязанных действий и операций, выполняемых автотранспортными предприятиями и их подразделениями самостоятельно или согласовано с другими организациями при подготовке, осуществлении и завершении перевозок груза. ...

Основы организации перевозок на железных дорогах
В теории и практике грузовой коммерческой работы железных дорог происходят существенные качественные изменения, которые являются логическим следствием ускорения темпов технического прогресса. Расширена сфера применения электронно-вычислительной технике решения задач планирование перевозо ...