Компоненты вектора yне ограничены по знаку, потому что прямая задача (1.21) каноническая. Неравенства двойственной задачи становятся нагляднее, если представить двойственный вектор yв виде ![]() , где первые m компоненты ui соответствуют строчным уравнениям (15), последующие n компонент uj – столбцовым уравнениям (16). Число ui принято называть потенциалом поставщика I, число uj – потенциалом потребителя j. Если в задаче (22) записать векторы y, b, c и матрицу А покомпонентно, то с учетом того, что каждый столбец матрицы А содержит всего две единицы, одна из которых соответствует строчному, другая – столбцовому уравнению прямой задачи, получим двойственную задачу в виде
, где первые m компоненты ui соответствуют строчным уравнениям (15), последующие n компонент uj – столбцовым уравнениям (16). Число ui принято называть потенциалом поставщика I, число uj – потенциалом потребителя j. Если в задаче (22) записать векторы y, b, c и матрицу А покомпонентно, то с учетом того, что каждый столбец матрицы А содержит всего две единицы, одна из которых соответствует строчному, другая – столбцовому уравнению прямой задачи, получим двойственную задачу в виде
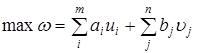 ; (23)
; (23)
![]() ,
, ![]() ,
, ![]() . (24)
. (24)
Из постановки двойственной задачи (23), (24) видно, что увеличение потенциалов ui и uj приводит к возрастанию целевой функции (23), так как по предположению ai>0, bj>0 для всех I, j. Однако неравенства (24) ограничивают рост целевой функции. Согласно им, сумма потенциалов поставщика и потребителя не должна превышать расходы на перевозку между ними единицы продукта. Более строго, из второй теоремы двойственности следует, что оптимальный план прямой задачи может включать ненулевое значение перевозки xij только в том случае, если сумма потенциалов поставщика I и потребителя j равна величине расходов на перевозку между ними единицы продукта. Применяя этот результат к паре задач (14) – (17) и (23), (24), получаем следующий признак оптимальности плана транспортной задачи: если план ![]() оптимален, то ему соответствует система
оптимален, то ему соответствует система ![]() чисел ui и uj, удовлетворяющих условиям:
чисел ui и uj, удовлетворяющих условиям:
![]() для
для ![]() ; (25)
; (25)
![]() для
для ![]() . (26)
. (26)
Введем для переменных xij оценки
![]() , (27)
, (27)
которые являются приведенными коэффициентами целевой функции, эквивалентными оценками ![]() симплекс метода. Тогда из (25), (26) получаем признак оптимальности в следующем виде: план
симплекс метода. Тогда из (25), (26) получаем признак оптимальности в следующем виде: план ![]() оптимален, если все его оценки
оптимален, если все его оценки ![]() вида (27) неположительны.
вида (27) неположительны.
Разновидностями транспортной задачи являются задача о максимальном потоке, задача о назначениях и т. д. При этом каждая разновидность транспортной задачи может решаться различными методами. Например, задача о назначениях кроме классического метода решения имеет так называемый венгерский метод.
При диспетчировании перевозок грузов в конкретном транспортном хозяйстве конкретного предприятия диспетчеру всегда приходится решать транспортную задачу, т. е. составлять план (расписание) перевозок грузов при минимальных затратах на их перевозку. Естественно, диспетчер составляет не всегда оптимальный план. Для реальной минимизации затрат на перевозку грузов необходимо использовать ЭВМ.
Технологический процесс изготовления изделий на предприятиях микроэлектроники является очень трудоемким, а организация производственного процесса требует большое и разнообразное количество сырья и материалов, поэтому для обеспечения бесперебойного и эффективного функционирования производства на предприятии необходимо наличие развитой структуры транспортного хозяйства, которое позволяет выполнять все необходимые перевозки грузов. Неоптимальное распределение грузовых потоков может привести к росту себестоимости конечной продукции, а, следовательно, и к ее неконкурентоспособности. Ввиду этого рациональное планирование грузовых перевозок играет немаловажную роль в эффективности работы всего предприятия. Организацией транспортных потоков на предприятиях занимается диспетчерская служба или диспетчер, а так как работа людей является субъективной и основывается на опыте и профессионализме человека (группы людей), то схема распределения грузовых потоков часто является неоптимальной. Поэтому при диспетчировании целесообразнее было бы использовать программный комплекс, работающий на алгоритме решения транспортных задач со многими неизвестными и возможностью включения новых пунктов сырья, материалов, потребителей и автомобилей.
Другое по теме:
Разработка оборудования для вырезки балласта на базе машины ЩОМ-Д
Балластная призма, на которую уложена рельсошпальная
решетка, может состоять из щебня, гравия, ракушечника и песка. На линиях с
большой грузонапряженностью и высокими скоростями движения поездов балластная
призма устраивается из щебня и отходов асбестовой промышленности. Толщина
балластн ...
Проектирование одноступенчатого редуктора с цилиндрическими прямозубыми эвольвентными зубчатыми колесами
Редуктор - это механизм состоящий
из зубчатых или червячных передач, заключенный в отдельный закрытый корпус.
Редуктор предназначен для понижения
числа оборотов и, соответственно, повышения крутящего момента.
Редукторы делятся по следующим
признакам:
- по типу передачи - на зубча ...
Проектирование системы управления гидравлическими приводами машины
Назначение, работа и устройство машины ВПР – 02
Машина ВПР-02 предназначена для выправки пути в
продольном профиле, по уровню и в плане, уплотнения балластной призмы под
шпалами и около их торцов при работах по техническому обслуживанию пути и при
новом строительстве. Машин ...
